KAN (Kolmogorov-Arnold Networks) | Harshwardhan Sanjay Fartale

1. Mathematical Foundations & Architecture

Kolmogorov-Arnold Representation Theorem: KANs are founded on a classic result by A. N. Kolmogorov and V. Arnold, which states that any continuous multivariate function can be represented as a finite superposition of univariate functions(A Comprehensive Survey on Kolmogorov Arnold Networks (KAN)). In practical terms, this theorem guarantees that for a function $f(x_1,\dots,x_n)$, there exist some continuous 1D functions $\{\Phi_q\}$ and $\{\Psi_{q,p}\}$ such that:

\[f(x_1,\ldots,x_n) \;=\; \sum_{q=0}^{2n} \; \Phi_q\!\Big( \sum_{p=1}^n \Psi_{q,p}(x_p) \Big)\,,\]

i.e. $f$ can be decomposed into inner univariate functions $\Psi_{q,p}$ (each depending on a single input variable $x_p$) and outer univariate functions $\Phi_q$ aggregated by addition. This theorem provides a constructive blueprint for function approximation using single-variable building blocks, which is the key inspiration for KANs

KAN Architecture - Instead of the traditional neuron model with linear weighted sums and fixed activations, a KAN implements the above idea by making each edge of the network carry a learnable univariate function. In other words, every connection between neurons is parameterized as a nonlinear function (originally chosen as a B-spline) rather than a scalar weight. Each neuron simply sums up the outputs of the incoming edge-functions. Formally, if $z_i^{(l)}$ denotes the $i$-th activation in layer $l$, then a KAN layer computes each output neuron $j$ as: (OpenReview) $z_j^{(l+1)} \;=\; \sum_{i=1}^{N_l} f_{ij}^{(l)}\!\Big(z_i^{(l)}\Big)\,,$

where $f_{ij}^{(l)}: \mathbb{R}\to\mathbb{R}$ is a learnable univariate function on the edge from neuron $i$ (layer $l$) to neuron $j$ (layer $l+1$). There are no separate linear weight matrices; the nonlinearity of $f_{ij}$ itself provides the transformation. In the shallowest case (two-layer KAN), this architecture directly mirrors Kolmogorov’s decomposition: the first layer learns inner functions $h_{p}(x_p)$ on each input dimension, and the second layer learns outer functions $g_q(\cdot)$ that combine those results Quanta Magazine.

Parameterized Functions (B-Splines): In practice, each learnable edge-function $f_{ij}$ is parameterized as a spline (often a B-spline) with a set of control points that can be tuned during training. B-splines are piecewise polynomial curves defined by control points, offering a flexible yet smooth basis for approximating arbitrary 1D functions. By adjusting the control points, the shape of the spline changes locally without affecting the entire function. This choice ensures the learned activation functions are smooth addressing potential non-smoothness in Kolmogorov’s original construction and stable to train. Each edge thus has multiple parameters (the spline control values) instead of a single weight. For example, a KAN might initialize each $f_{ij}$ as a near-linear spline and then let training mold each into the required nonlinear shape. This edge-centric design lets KANs dynamically adapt their activation functions to the data, rather than relying on a fixed function like ReLU or tanh.

Illustrative Pseudocode: The following pseudocode contrasts a single layer of an MLP vs. a KAN:

Comparison of MLP Layer with KAN Layer in Pytorch

In the KAN layer, f_ij is a learned function (e.g. a spline) specific to edge $(i\to j)$, replacing both the weight and the neuron’s activation for that connection. The neuron simply aggregates these contributions (here via summation). Deep KANs can be built by stacking such layers, allowing composition of these univariate transformations across multiple levels.

2. Comparison with MLPs

Structural Differences: Traditional Multi-Layer Perceptrons (MLPs) use linear weights and fixed activation functions at neurons, whereas KANs use no linear weights at all – every “weight” is replaced by a flexible function on the input signal. In effect, MLPs learn parameters for nodes (the weight matrix between layers is trained, then a fixed nonlinearity like ReLU is applied), while KANs learn parameters for edges (each connection has a trainable nonlinear mapping). This leads to a duality: MLP = fixed nonlinearity + learned linear weights; KAN = fixed linear sum + learned nonlinear functions. The figure below (from Liu et al. 2024) illustrates this difference, highlighting that MLPs apply activations at neurons (circles) whereas KANs apply learned functions on each connecting edge before summing.(GitHub - KindXiaoming/pykan: Kolmogorov Arnold Networks)

Source: Liu et al. (2024)

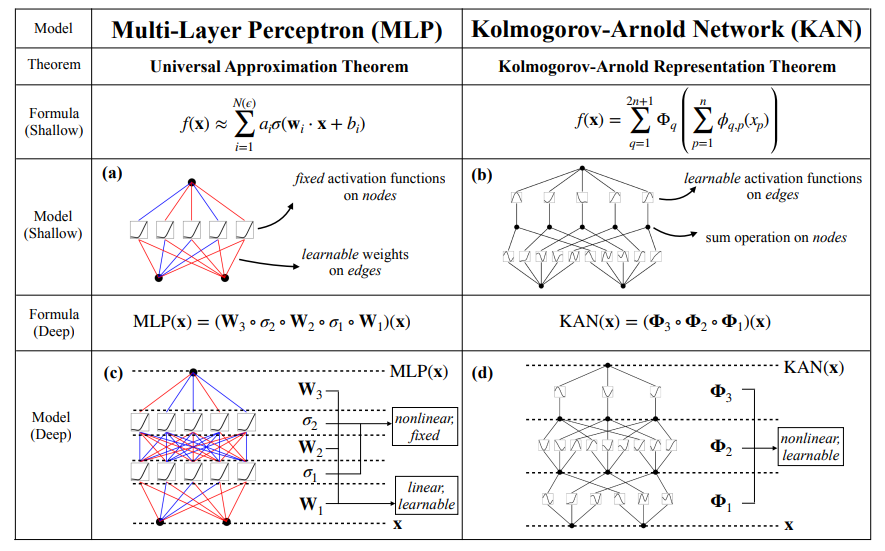
Learnable Functions vs Fixed Weights: In an MLP, the transformation from layer to layer is $\sigma(Wx + b)$, with $\sigma$ (e.g. ReLU) fixed and $W,b$ learned. In a KAN, the transformation is $\sum_i f_i(x_i)$ (plus bias if needed), with each $f_i$ being learned and no separate $W$. Essentially, KANs “allocate” more flexibility per connection, whereas MLPs rely on combining many fixed nonlinear units to build complexity. This means KANs move the bulk of learnable parameters into the activation functions themselves, often resulting in fewer total connections needed than an equivalent MLP (Trying Kolmogorov-Arnold Networks in Practice).

Expressive Power (Universal Approximation): Both MLPs and KANs are universal function approximators, but via different theorems. MLPs leverage the Universal Approximation Theorem (with enough neurons, an MLP can approximate any continuous function on a domain), while KANs directly leverage the Kolmogorov-Arnold (K-A) theorem to construct such approximations. In theory, a single hidden-layer KAN with sufficiently complex edge functions can exactly represent any continuous function (the K-A theorem provides an existence proof), whereas an MLP might require many more neurons or layers to approximate the same function with fixed activations. KANs thus excel at modeling functions with complex or “spiky” behavior in each input dimension, because each edge can carve out a detailed univariate relationship. In practice, KANs implement the K-A decomposition explicitly, using B-spline basis functions to approximate the required univariate mappings. This can translate to greater expressivity per parameter.(Revolutionizing Language Models with KAN: A Deep Dive - Association of Data Scientists).

Parameter Efficiency & Neural Scaling: A striking reported advantage is that much smaller KANs can achieve accuracy comparable or superior to much larger MLPs on certain tasks. Each KAN edge function (with, say, $k$ control points) can encode a nonlinear relation that an MLP might need multiple neurons and layers to capture. Empirically, Liu et al. (2024) found KANs follow faster neural scaling laws – the error decreases more rapidly as model size increases, compared to MLPs. In other words, to reach a given accuracy, a KAN required fewer trainable parameters than an MLP in their tests. The flexibility of splines allows KANs to fit complex patterns without blowing up the network width/depth. One study noted that KANs can match MLP performance at equal parameter counts, and sometimes exceed it, though they require careful tuning (Trying Kolmogorov-Arnold Networks in Practice). The original KAN paper demonstrated that a KAN with significantly fewer nodes could outperform a dense ReLU network on function-fitting benchmarks.

Continuous Learning and Locality: Because each KAN weight is a localized function (with local control points), learning in a KAN can be more localized. This has implications for continual learning. In standard nets, fine-tuning on new data often alters weights globally and can erode old capabilities (catastrophic forgetting). In KANs, adding new data primarily adjusts the spline control points in relevant regions of the input space, leaving other regions (and other functions) mostly unchanged. For example, if a KAN-based language model learns a new vocabulary or coding style, only certain edge-functions for those inputs might reshape, while others retain their previously learned shape. This property means KANs can integrate new knowledge without overwriting all weights, potentially enabling more seamless continual learning. MLPs, by contrast, have distributed representations where a single weight doesn’t correspond to an isolated input relationship, making targeted updates harder.(Revolutionizing Language Models with KAN: A Deep Dive - Association of Data Scientists)

Interpretability: A major motivation for KANs is interpretability. In an MLP, each weight by itself is usually not meaningful, and neurons combine many weights making interpretation difficult. In a KAN, each edge’s function $f_{ij}(x)$ can be visualized as a curve, directly showing how the input from neuron $i$ influences neuron $j$ across the range of values. After training, one can extract these learned univariate functions and inspect them.They might correspond to intuitive relations (e.g. an edge function might learn a sinusoidal shape if the output depends sinusoidally on an input).This transparency is especially useful in scientific or engineering tasks where understanding the learned model is as important as its accuracy. MLPs lack this fine-grained interpretability, since their learned mapping is entangled across many parameters. Thus, KANs offer a more human-understandable model: as the saying goes, they turn the “black box” into a collection of readable 1D transformations.

Summary: KANs and MLPs both approximate complex functions, but KANs do so by baking learnable math into the connections. This difference yields advantages in function approximation fidelity, parameter efficiency, and interpretability. However, it also comes with computational challenges (will uupdate later). In essence, KANs can be seen as a new paradigm: they trade the simple, generic structure of MLPs for a structure with built-in mathematical richness (the Kolmogorov-Arnold basis). This seemingly small change – moving from scalar weights to learned functions – has profound implications on how the network learns and what it can represent (GitHub - KindXiaoming/pykan: Kolmogorov Arnold Networks).

The original paper can be found here

Last Updated - 25/02/2025